【一陸技】工学A 令和5年1月期第1回 A-1 解説
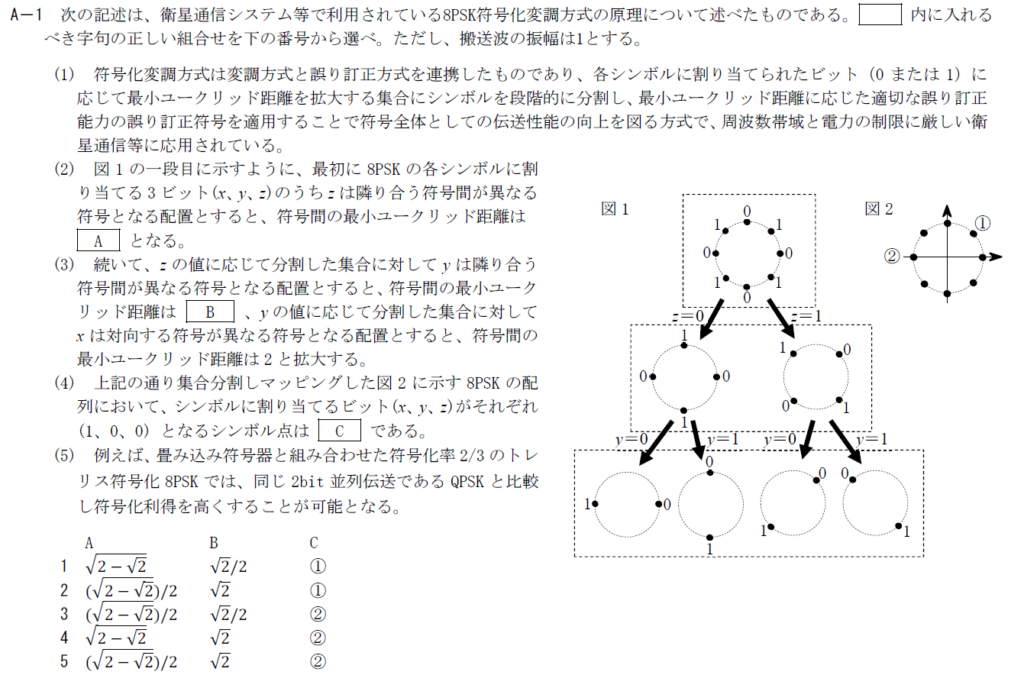
8PSKの問題。図が仰々しいので面食らうかもしれないが、文章をよく読んで計算すれば解ける。完全に理解できなくてもOK。
[A]
図1の1段目を見ろと書いてあるのだから見ましょう。色々ゴニョゴニョ言ってますが、「符号間最小ユーグリッド距離」、つまり単に幾何的な距離を求めればいい話。
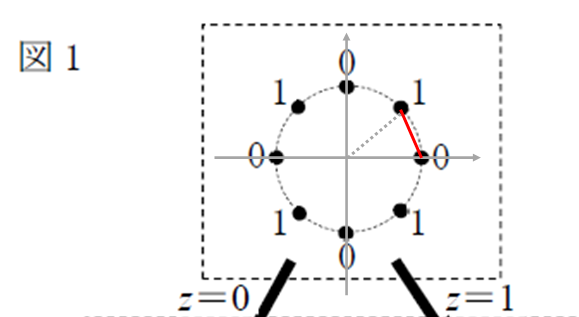
問題文の冒頭で、搬送波の振幅は1とあるので半径1と考える。45°の弦の長さなので余弦定理より、
x^2 = 1^2 + 1^2 -2*1*1*cos(45°)
∴x=√(2-√2) ■
[B]
次は2段目の図を見て、同じように符号間の幾何的な距離を求めればOK。
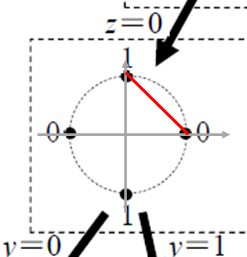
こちらは余弦定理を使うまでもなく、√2 ■
[C]
実はここまでで答えが分かってしまうが、一応さらっとやっておく。
文章をよく読むと、「(x,y,z)がそれぞれ(1,0,0)となるシンボル点」と言っているので、図でz=0,y=0をたどっていけば、以下の図のどちらかの点だとわかる。x=0,1がどちらに対応するかはここでは定義されていないのでわからないが、図2の①②の中では、②しか当てはまらない。
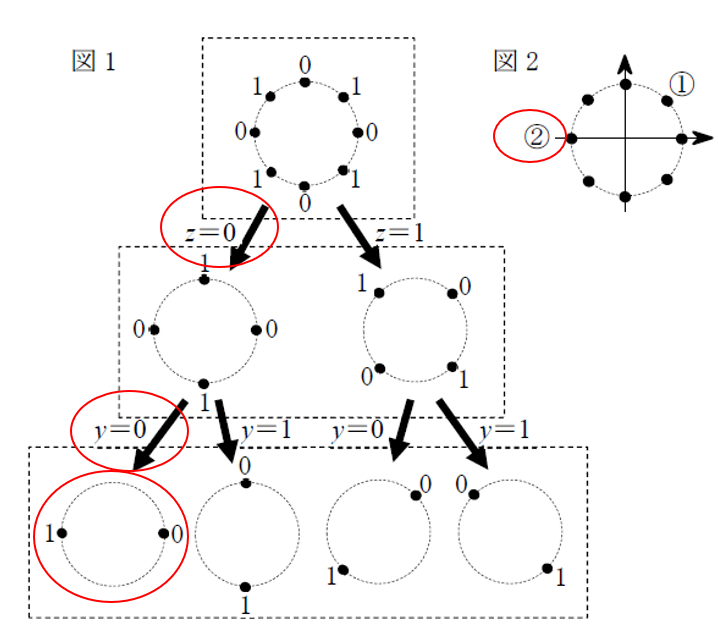
よって答えは4だ。
※ちなみに、信号理論においては「符号間最小ユーグリッド距離」のほかにも「ハミング距離」というのも存在する。
この問題の背景知識
この問題背景知識には、集合分割法、符号化変調方式といった内容が含まれている。符号理論においてエラー率低減のための策の一種であるが、理論的なことをしっかり理解するのは非常に難しいため、背景だけ簡単に整理しておく。
集合分割法とは
端的に言うと、位相図(コンスタレーション/Constellation)へのビットの並べ方の一種である。QPSKを例にとって説明する。
QPSKは2bitの2進数 00, 01, 10, 11を、搬送波1*cos(ωt)の位相を変えたもの:1*cos(ωt + 0)、1*cos(ωt + π/2)、1*cos(ωt + π)、1*cos(ωt + 3π/2) に対応させた変調方式である。
しかしこの対応付けはこの順番である必要はない。以下の図のように割り当ての順番にはいろいろポリシーがあり、有名なものには名前がついている。ここではバイナリコード、グレイコード、集合分割法の3種類を挙げた。
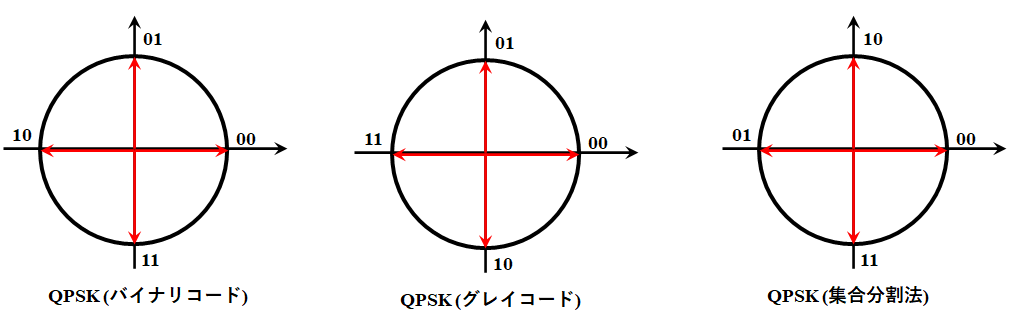
バイナリコード、グレイコード、集合分割法でそれぞれ特徴が異なる。
バイナリコード
バイナリコードは、2進数00,01,10,11を順番通りに0,π/2,π,3π/2に対応付けたもので一番単純な割り当て方法である。簡単で分かりやすいのだが、以下の図のように、シンボル点が1つ隣に移ってしまっただけで2ビット分の符号が一気に変わってしまうパターンがある。ビット誤りというのは隣接するシンボル点と間違えてしまうことにより発生するので、ビットエラー率が高くなってしまうデメリットがある。
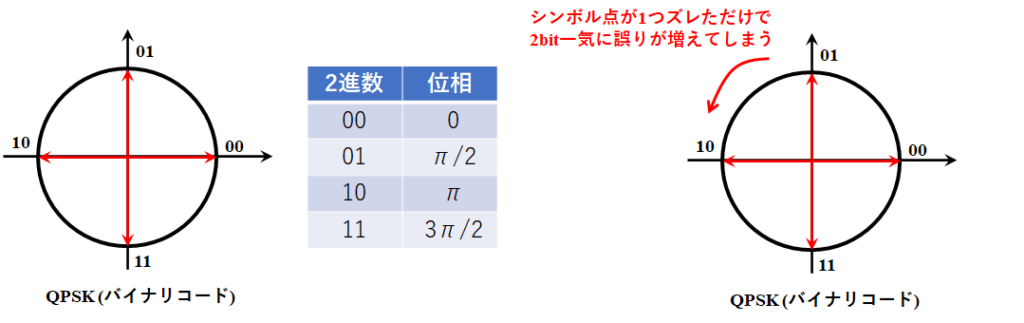
グレイコード
グレイコードはバイナリコードの弱点を補強するため、シンボル点が1つ隣にズレてもbit誤りが1bit分だけになるように、2進数00,01,10,11の並べ方を工夫したものである。以下の図を見ると、1シンボル隣に移ってもbitの変化は1bit分しかないことが分かる。よってバイナリコードと比べて、ビットエラー率を低くすることができる。
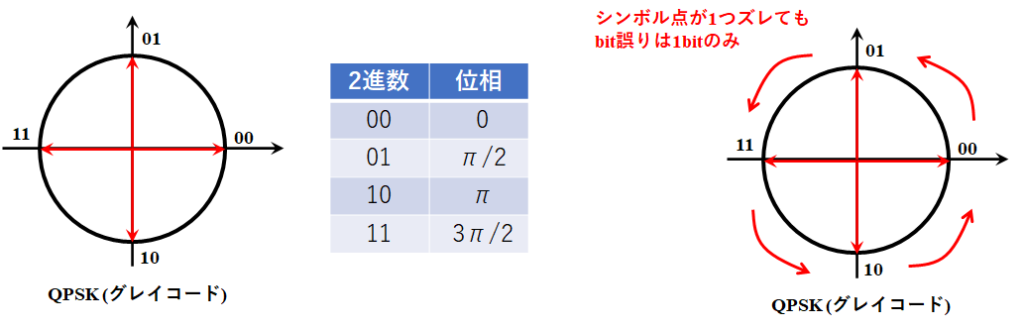
集合分割法
2bitの2進数のMSBから順に1bitずつ多段階復調することが前提の並べ方である。多段復調すること後段になればなるほど符号間のユーグリッド距離(単なる幾何的な距離)は増加する。この段階ではまだbit誤り率には寄与しない。この集合分割法の並べ方と誤り訂正符号を組み合わせた符号化変調方式というものを用いることでグレイコードよりビット誤り率を低減することができると知られている。
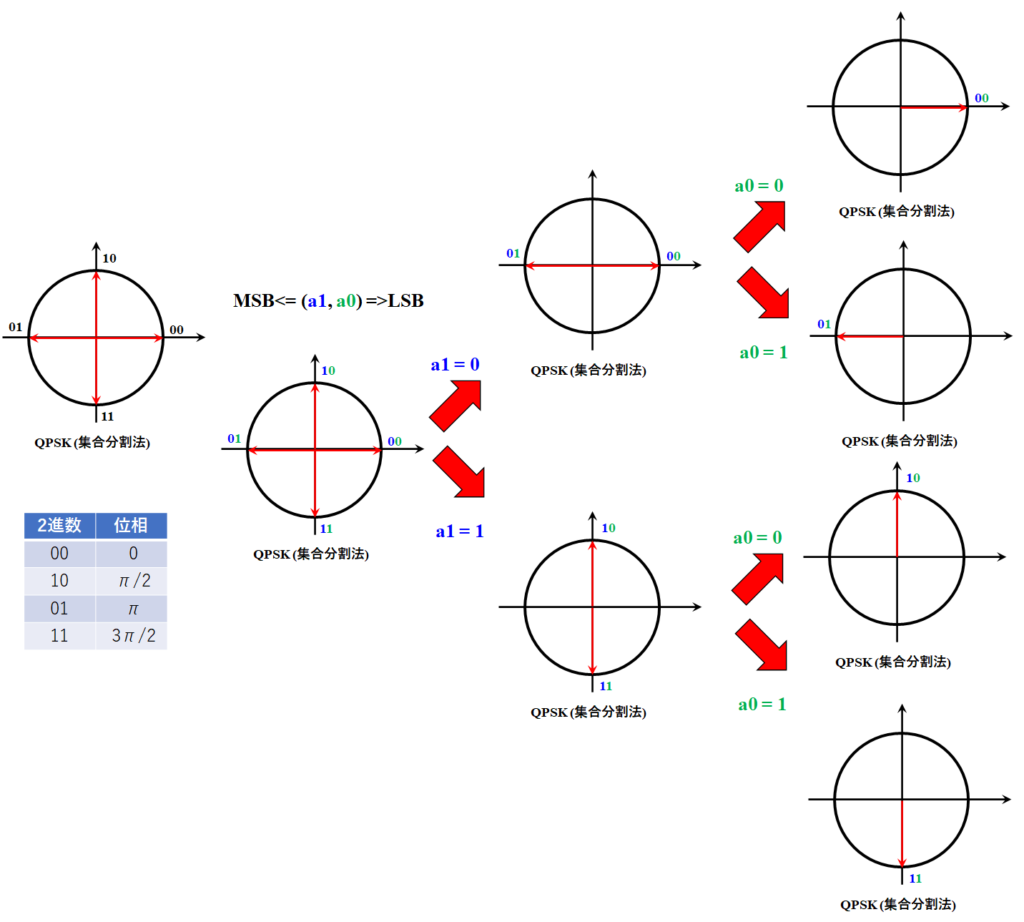
符号化変調方式とは
符号化変調方式とは変調方式と誤り訂正方式を一体化したものである。上で説明したように、集合分割法を用いるとMSBからの段階的復調によって符号間ユーグリッド距離を大きくすることができる。ユーグリッド距離が大きくなると、誤り訂正用の冗長ビット長も少なくて済む。このユーグリッド距離に応じで冗長ビットの長さを適切に設定すれば、効率よく誤り訂正ができ、結果的にトータルのビット誤り率を減らすことができる、という手法である。
多値変調と畳み込み符号(冗長ビットの作り方の一種)を組み合わせた方式をトレリス符号化変調方式という。
参考文献
符号理論の教科書PDF
符号理論はほとんど数学の分野に近く、理解するのが非常に難しい。本屋で書籍を購入してもよいがネット上にはありがたいことに無料で閲覧できるPDF教科書がいくつかある。筆者も本ブログ執筆時点ではほとんどアプローチできていない分野であるが、折に触れて学習を進めていこうと思っている。ここでは筆者が見つけた無料PDF教科書のリンクを紹介する。
また、誤り訂正符号について簡単な具体例を用いながら解説してくれている近畿大学の解説サイトがあったのでこちらも共有しておく。生成行列やパリティ検査行列など、難しい内容を具体例で説明してくれており非常にとっつきやすい。
