【一陸技】工学A 令和5年1月期第1回 A-11 解説
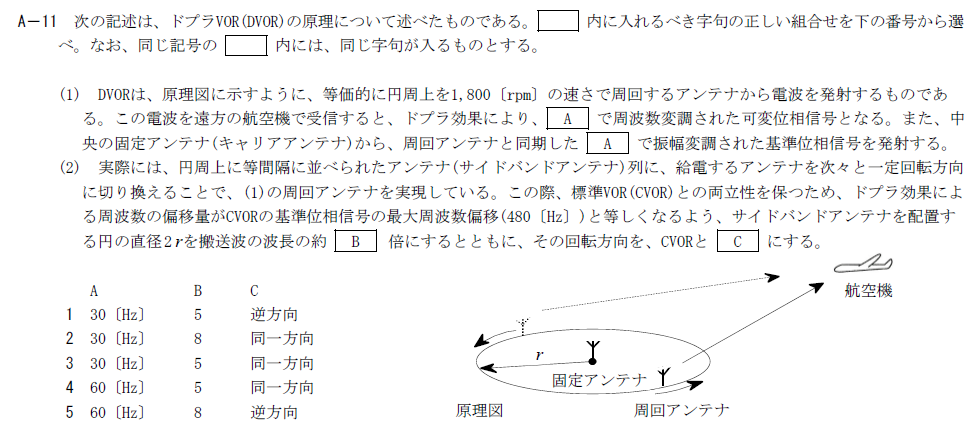
Doppler VORの問題であり昔から出題されている問題である。
この問題は、光のドップラー効果の公式を知ったうえでそれなりに計算しないと答えを出せないが、一陸技では割とそのまま出題されるし、試験時間中にやるよりは覚えておいた方が早い。まず、覚えるべき事項を端的に述べてから、詳しい導出過程を述べる。
DVORで覚えておくべき事項
■ DVORは円周上を1800[rpm]でアンテナが回る。[rpm]=1分当たりの回転数。よって角速度はω=2π[rad]×1800[回転/min]÷60[s/min] = 2π×30[rad/s]。周波数は30[Hz]。
■ アンテナの接線方向の速度は、v = rω で計算できる。
■ 送信アンテナが速度v=rωで動きながら電波を出すので、飛行機が受信する電波はドップラーシフト Δf = (v/c) f送信 分だけ周波数が変わる。飛行機にアンテナが近づくときは周波数が上がり、飛行機から遠ざかるときは周波数が下がる。
■ ドップラーシフトが周期的(角速度ωで)に起こるため、飛行機が受信する電波の周波数は、FM変調されるように見える。変調周波数 fs = 30[Hz]である。
■ DVORは少し仕組が違う標準VORから派生したもの。標準VORの最大周波数偏移がΔF = 480[Hz]の設定になっているので、DVORもそれに合わせるために、2r ≒ 5λ送信波 という設定になっている。
■ DVORのアンテナが動く向きは、標準VORの逆である。
正直、これだけ覚えていればこの手の問題は解けて、実際この問題の答えは1となる。
しかし、なぜそうなるのか気になるし、単純な暗記は理系人間にとって苦痛だと思うので、以下では丁寧に数式で議論していきたいと思う。
ドップラーシフトの公式
軸の取り方が重要。図のように、送信機が左にあり受信機が右にあり、送信機→受信機の方向にx軸を取る。受信機が送信機に対して相対速度vで遠ざかっている場合、受信機が感じる周波数は次のようになる。
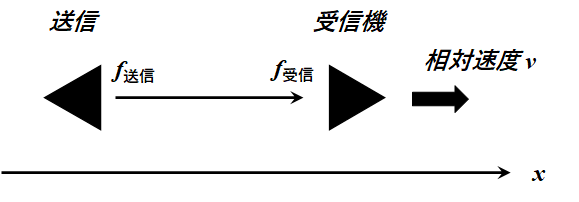
\(f_{送信} = f_{受信} × \sqrt{\dfrac{1-\frac{v}{c}}{1+\frac{v}{c}}} ≒ f_{受信} (1-\frac{v}{c}) \)
DVORの受信周波数の計算
DVORの構成は以下の図のようになっている。無変調の電波 f送信 が半径rの円上を反時計周りに回っている。円の中心では30HzでAM変調された電波が送信されている。回転の角速度は上で計算した通り、ω = 2π×30[rad/s]となる。また、飛行機は速さVでDVORの系に向かっている。
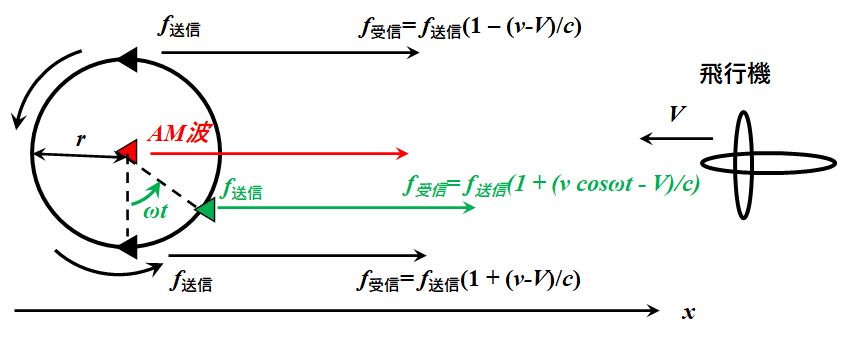
図で丁度ωtのところに位置した送信機から出た電波は、ドップラーシフトにより以下の受信周波数となる。
f受信= f送信(1 + (v cosωt – V)/c) = f送信(1 –V/c ) + f送信(rω/c)cosωt
一方で、FM変調された周波数は教科書通りの式にすると、
fFM = fc + ΔFcosωst
この2式を比較すると、
- キャリア周波数 fc = f送信(1 –V/c )
- 最大周波数偏移 ΔF = f送信(rω/c)
- 変調周波数 ωs = ω = 2π×30[Hz]
のFM波になる。
標準VORとの整合
標準VORは最大周波数偏移が480Hzなので、DVORもそれに合うようにrを定める必要がある。上の式より、
ΔF = f送信(rω/c) = 480[Hz]
2rf送信/c = 480×2/ω
2r/λ送信 = 480×2/(2π×30) =5.095.. ≒ 5
よって、直径は送信波長のおよそ5倍となる。
また、標準VORとDVORは回転するアンテナに違いがある。
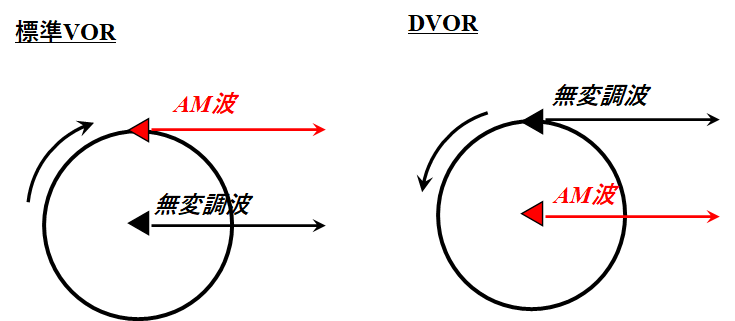
標準VORはAMアンテナの方が時計回りに回転する。つまりAMアンテナから見れば無変調波のアンテナは相対的に反時計回りに回転しているように見える。そのため、DVORが標準VORに整合させるには、逆向きに回転させねばならない。
以上
