【一陸技】工学A 令和5年1月期第1回 A-18 解説
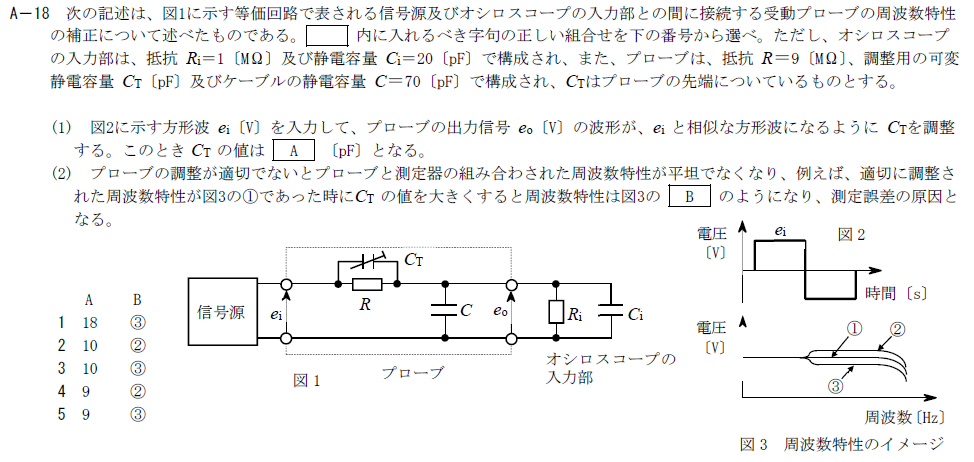
オシロスコープの受動プローブの周波数特性の補正の問題である。信号源の電圧がei、プローブ入力部の電圧がeoだとすると、eo/ei が実数となればプローブ含めた回路全体にリアクタンス成分が存在しないことになるので、波形eoと波形eiに差が出なくなる。リアクタンス成分を調整して全体として0にするために、可変静電容量CTが用意されているのである。
(1)
さて、まずは図1の回路においてeo/ei の比を求めたい。eoは、eiを合成インピーダンス1(CT, R)と合成インピーダンス2(C, Ri, Ci)で直列分圧している。ここで、
合成インピーダンス \( Z_{1} = \dfrac{1}{ 1/R + jωC_{T}} \)
合成インピーダンス \( Z_{2} = \dfrac{1}{ 1/R_{i} + jω(C_{i} + C)} \)
であり、
\( \dfrac{e_{o}}{e_{i}} = \dfrac{Z_{2}}{Z_{1}+Z_{2}} = \dfrac{1}{1+\dfrac{Z_{1}}{Z_{2}}} = \dfrac{1}{1+\dfrac{1/R_{i} + jω(C_{i} + C)}{1/R + jωC_{T}}} \)
一般に、複素数 \( \dfrac{a+jb}{c+jd} \) が実数になる条件は、\( ad – bc = 0 \) のため、
\( \dfrac{1}{R_{i}}×ωC_{T} \,\,–\,\, ω(C_{i}+C)×\dfrac{1}{R} = 0 \)
\( C_{T} = \dfrac{R_{i}}{R}(C_{i}+C) = \dfrac{1M}{9M}(20p+70p) = 10[pF] \) ■
(2)
CTが調整できていないとどうるか?という問題。ここはコンデンサの役割と高周波の流れを定性的に考えると解きやすい(変に数式で計算すると、計算地獄になる。。。)
まず、コンデンサとは高周波成分を通しやすく、容量が大きければ大きいほど通しやすくなり小さければ通しにくくなる。そしてコンデンサCTは信号源の上部端子からの高周波を通す役割を担っている。すなわち、CTが大きすぎると後段に高周波が過剰に流れてしまい、小さすぎると高周波がほとんど流れなくなり、不足状態となる。
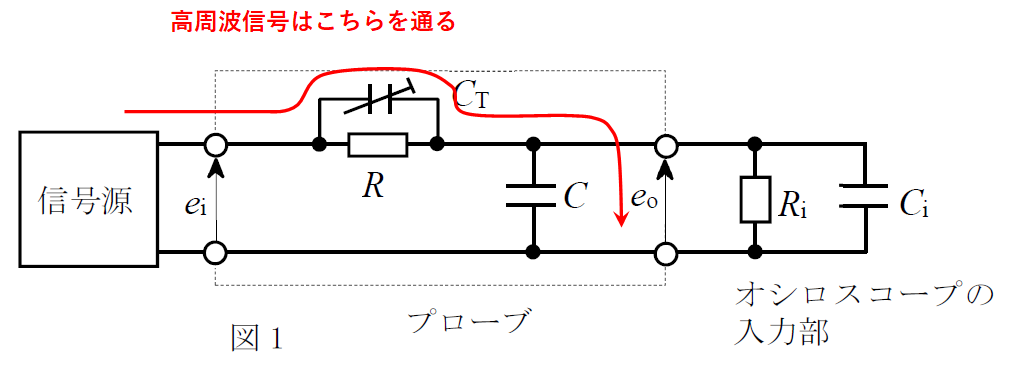
さて、問題文では、『CTを大きくすると』とあるので、高周波は後段により流れやすくなる。そうなると周波数特性としては、周波数の高い側が盛り上がる。よって周波数特性グラフは②のようになる。
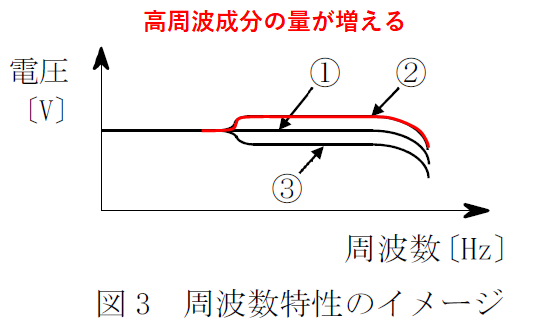
ちなみに時間波形は高周波成分をより含むようになるので矩形のエッジの部分でピュンと飛び跳ねるような形になる。一陸技ではこちらが問われることもあるのでしっかり押さえておきたいところだ。
以上で答えは2である。
