【一陸技】工学A 令和5年1月期第1回 B-5 解説
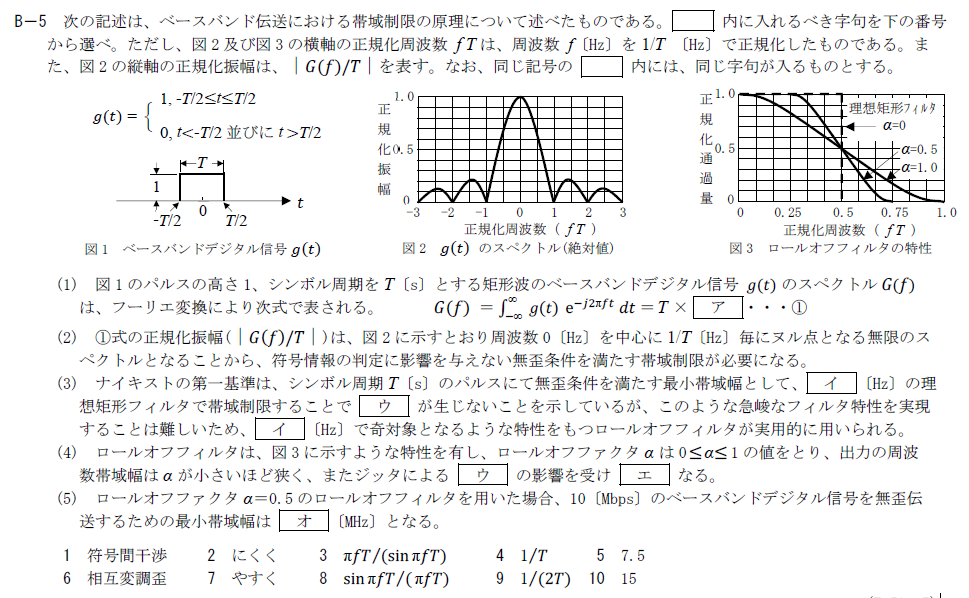
デジタル信号の時間波形は、図1のg(t)のように矩形波である。しかし矩形波というのはエッジのところが急峻に変化するため、高周波が多く乗ってしまっている。この矩形波をフーリエ変換すると、図2のようなsinc関数のスペクトルG(f)が得られる。sinc関数\(sinc(x) = sinx/x\)を見てわかるように、山がメインローブの隣サイドに無限に連続するため、高周波になることが分かる。
\( G(f) = \int_{-∞}^{∞} g(t)exp(-j2πft) dt = \int_{-T/2}^{T/2} exp(-j2πft) dt = Tsinc(πft) \)
[ア]=8
sinc関数のように周波数帯が広いと、帯域を無駄に使ってしまうので、時間波形g(t)を大幅に崩さない範囲で、スペクトルG(f)に窓関数R(f)を掛算してやり、高周波成分を小さくしてやる必要がある。
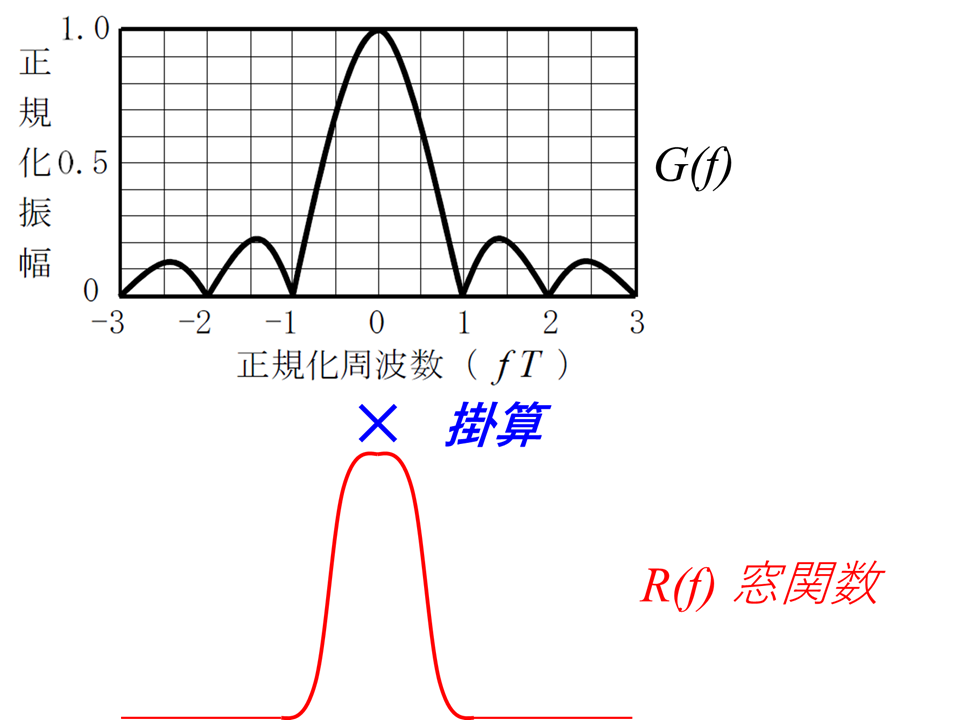
しかし、周波数領域でスパっと切断してしまうと時間領域の波形が逆にt = ±∞ までリンギングを起こしてしまう。リンギングを起こすと、隣のシンボルにしみこんでしまって、符号間干渉を起こしてしまう。
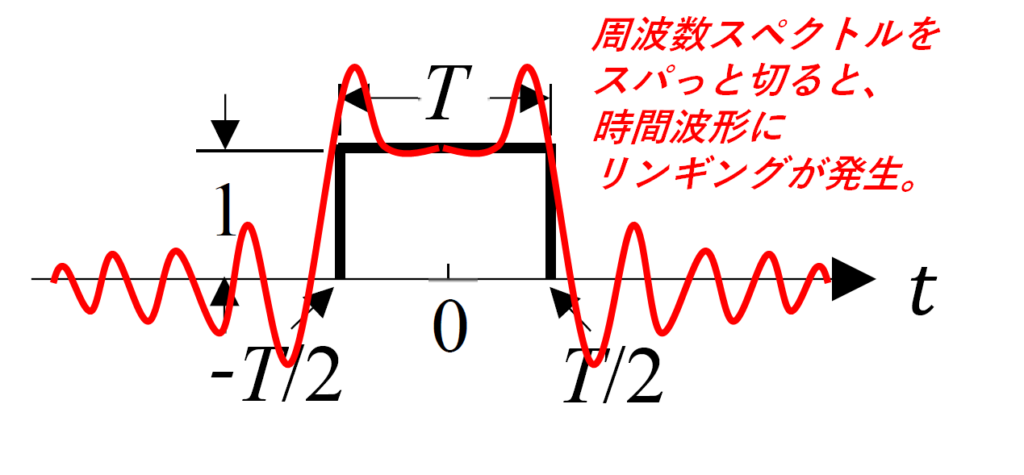
しかし!スパっと周波数窓で切る場合でも、ある狭い範囲に限るとリンギングも影響ににくく、0,1の情報も失われないようにできる。それが無歪条件と呼ばれるもので、シンボル周期をT[s]としたとき、周波数窓の幅を1/2T [Hz]以内にするというものである([イ]=9)。この条件なら符号干渉も起こらない([ウ]=1)。
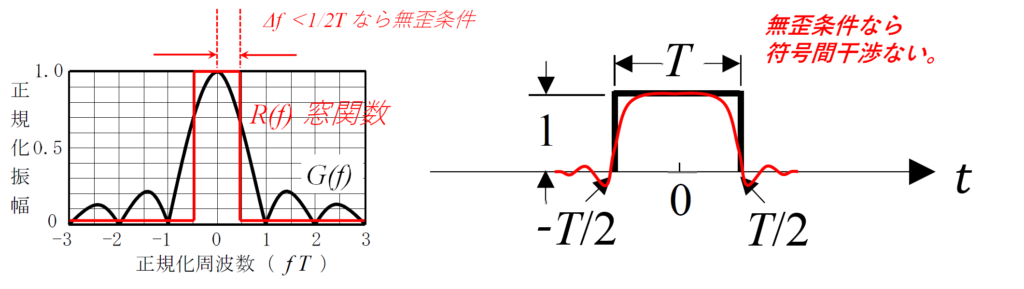
しかし、現実のフィルターではアナログであろうがデジタルであろうが、上記のようにスパっと切断する急峻なフィルターは作れない。あくまで数式上のフィルターである。
そこで一般的に実用で使われているのは、コサインの滑らかなカーブを利用したロールオフフィルターだ。ロールオフフィルターの関数定義は以下である。
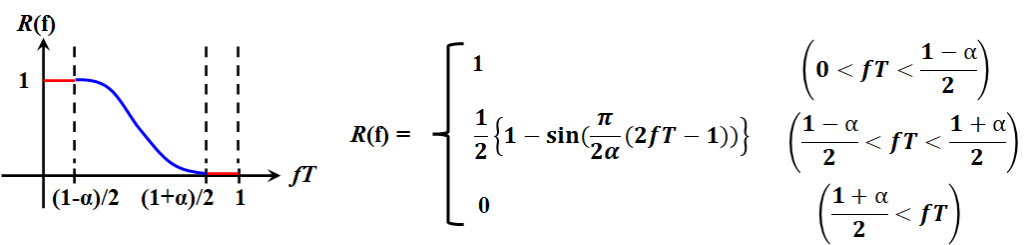
αはロールオフファクタと言われ、αが小さいと窓の傾きが急峻になり狭くなる。当然、狭くなるとリンギングの影響が大きくなり、ジッタによる符号間干渉の影響を受けやすくなる([エ]=7)。
α=0.5の時、1/T =10MHz (=10Mbps) のロールオフフィルタのカットオフ周波数は、グラフより
fT = (1+α)/2
∴ f =(1+α)/2T = {(1+0.5)/2 }*10MHz) = 7.5[MHz] ([オ]=5)
