無線工学【公式・導出】トランス(変圧器)の基本 ~ 符号・巻数比・回路方程式~
トランス(変圧器)・インダクタの公式 の難しさ
一アマ、一陸技、電検に限らず多くの電気系の資格試験や実務で登場するトランス・インダクタ。基本的な公式は、一般の参考書にも多く載ってるし、ネットにも解説記事が多く存在する。
しかしトランスや誘導起電力の分野で一番ややこしいのが符号の付け方だ。流儀もいろいろあるしネットや書籍の記載も間違っているものもある。符号の理解が肝の分野でもあるのだ。
また、トランスの巻き数比に関する公式も結果だけ記して導出方法を丁寧に書いていないネットの記事が散見される。導出の際には、あまり表立って記載されない暗黙の前提があるのでそこを理解しておく必要がある。筆者もこの分野を勉強する際、非常に悩まされた。
そこで本記事では、符号の付け方や導出方法を省略せずに、また、根幹となる少ない公式から導いてみる。
磁場H, 磁束密度B, 透磁率μ, 磁束φなどの物理量の関係式
まず登場してくる基本的な物理量を確認しておく。ここで注意してみてほしいのが、磁束\(φ\)と磁束鎖交数\(Φ\)である。同じギリシャ文字の大文字と小文字なので間違いやすいところだ。
ここに載っているものは基本的に暗記してください。
真空の透磁率 \( {μ}_{0} \)
物質の比透磁率 \( {μ}_{r} \) …真空の透磁率に対して何倍かを表す比
物質の透磁率 \( μ= {μ}_{r} {μ}_{0} \)
磁束密度 \( B=μH \)
磁束 \( φ=BS \)
磁束鎖交数 \( Φ=Nφ \)
公式集
さて、具体的なトランスにかかわるところの公式を見ていこう。
ここで重要なのは暗記するべき公式とその場で導出すればいい公式を分けて考えておくことである。
以下では、導出を与えていない公式は基本的に暗記するべきと考えてほしい。もちろんこれらの公式も物理の基本原理から導出は可能だが、試験会場や実務のその場において導出することは得策でないくらい導出が複雑だからだ。その辺はうまく割り切ろう。
N巻コイルに電流Iを流した時に発生する磁場 ←暗記
\( H=\dfrac{N}{ℓ}I\)
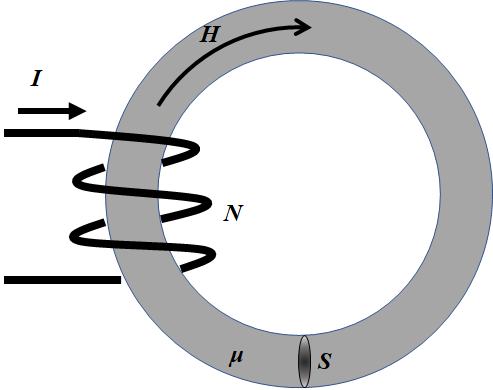
ただし、他の公式とごっちゃになったりどうしても忘れてしまった場合は、アンペールの法則から導出しよう。以下に示す。
アンペールの法則からの導出
\(∇・H=j\) つまり \(∫H・dℓ= I\) これが意味するとことは、磁場\(H\)を1周集めたら、中心に貫く電流\(I\)の垂直成分の絶対値に等しくなるということである。しかし上の図では、一見、電流\(I\)がクルクル回転しているように見えるので、以下のようにコイルが存在する局的な部分にフォーカスして考える。
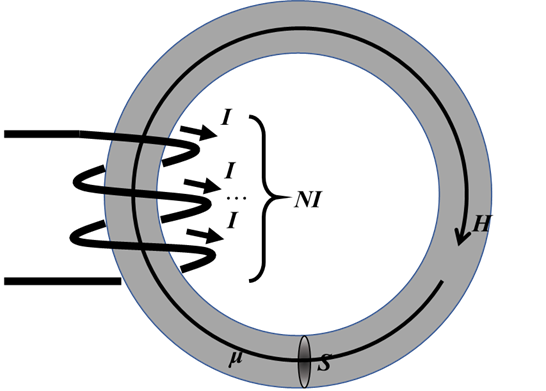
すると、回転する磁場\(H\)の中心に電流\(NI\)が貫いているように見える。この形でアンペールの法則を適用すれば、\(H・ℓ=NI\)
\(∴H=\dfrac{NI}{ℓ}\)
N巻コイルに電流Iを流した時に発生する磁束鎖交数とリアクタンスLの関係 ←暗記
\( Φ=Nφ=LI \)
ここで初めてリアクタンス\(L\)が登場してくるが、本来ここの公式はファラデーの電磁誘導の法則\( V=N\dfrac{dΦ}{dt} \)を用いて導出することになる。しかし意外とややこしいので暗記するのが得策。
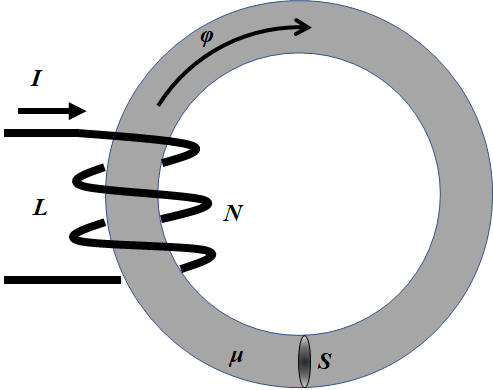
N巻きコイルのリアクタンスL
\( H=\dfrac{N}{ℓ}I\) と \( Nφ=LI \) より、L=に関して解いてIを消去すると、
\( L=μ \dfrac{N^2 S}{ℓ} \)
これは暗記不要。本来、\(L\)は\(I\)に依存しない値なので、上の2つの公式から\(I\)を消去すればいい。
トランスの相互インダクタンス(結合係数:k) ←暗記
\( M=k \sqrt{L_{A}L_{B}} \)
ここで、 \( L=μ \dfrac{N^2 S}{ℓ} \) の公式を用いてLを消去すると、
\( M=k μ \dfrac{{N}_{A}{N}_{B} S}{ℓ} \)
こちらは暗記不要である。
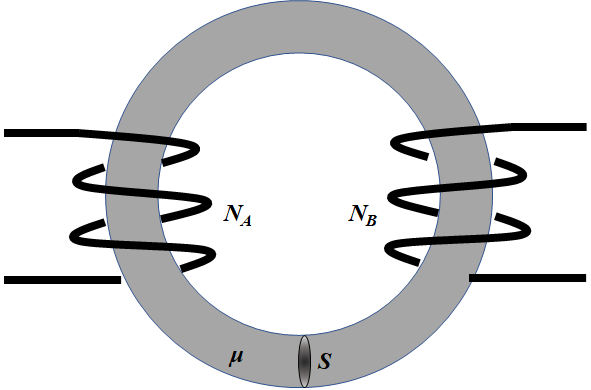
直列合成のL ←暗記
\( L_{合成}=L_{A}+L_{B}±2M \)
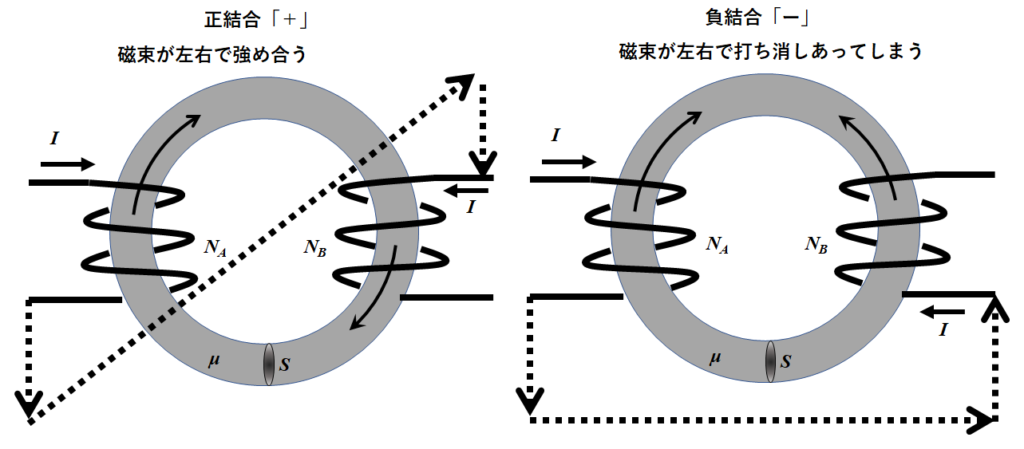
※正結合か負結合かは、問題文の絵のコイルの向きから判断する。
重要なのは設定した\(I\)の正方向に電流を流した時、左右の磁束の向きが同じなら正結合\(+M\)、逆方向なら負結合\(-M\)である。
ここで、 \( L=μ \dfrac{N^2 S}{ℓ} \) の公式を用いてLを消去すると、
\( L_{合成}=L_{A}+L_{B}±2M=μ \dfrac{({N}_{A}±{N}_{B})^2 S}{ℓ} \)
ちなみにこちらの式は暗記不要。
コイル内の電流が変化したとき、コイル両端で発生する誘導起電力 ←暗記
\( {V}_{自己}=L \dfrac{dI}{dt} \)
\( {V}_{相互}=M \dfrac{dI}{dt} \)
この式には符号は入れていない。なぜなら符号というのは、どこからどこの電位差かという定義によって変わってくるからである。実際の符号は、以下のように図を書いたうえで、キルヒホッフの式を書くときに意識すべきことである。
※自己誘導起電力の向きは、常に電流Iを妨げる方向に矢印を書く。
※相互起電力の向きは正結合、負結合で変わってくる。正結合であれば自己誘導と同じ向き、負結合であれば自己誘導と逆向きである。
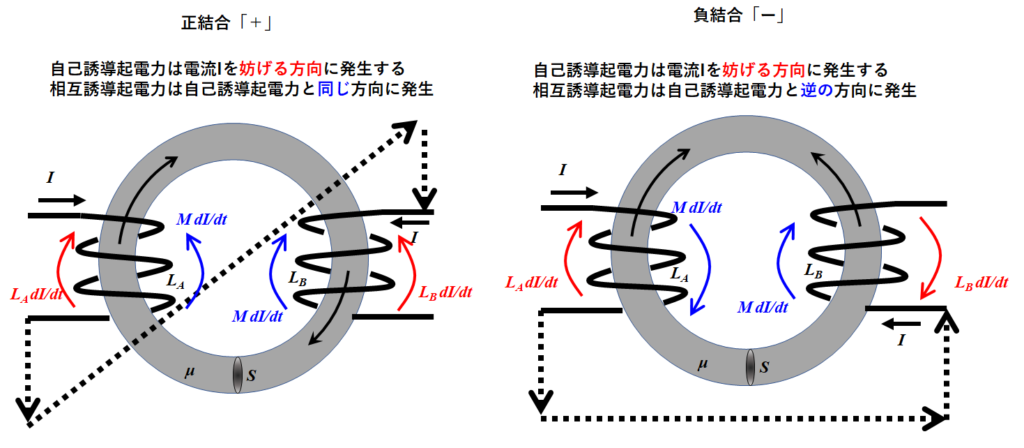
トランスでのキルヒホッフ式
\({I}_{A}\)、\({I}_{B}\)の正の向きを以下の図のように設定する。仮に、\({I}_{A}\)、\({I}_{B}\)に正の電流を流した時、双方から発生する磁束の向きが一致すれば、正結合、逆向きであれば負結合となる。本来は、\({I}_{A}\)を流すから\({I}_{B}\)が発生するのであって、”\({I}_{B}\)に正の電流を流したなら”という言い方は違和感があると思う。が、仮に\({I}_{B}\)に負の電流が流れたとしても、方程式上は\({I}_{B}<0\)で辻褄があうので問題ない。
この時の\(M\)の符号は、自分が設定した\({I}_{A}\)、\({I}_{B}\)の向きによって変わってくる。どんな定義にしてもいいが、以下の図のように設定したときの符号の決め方を説明する。
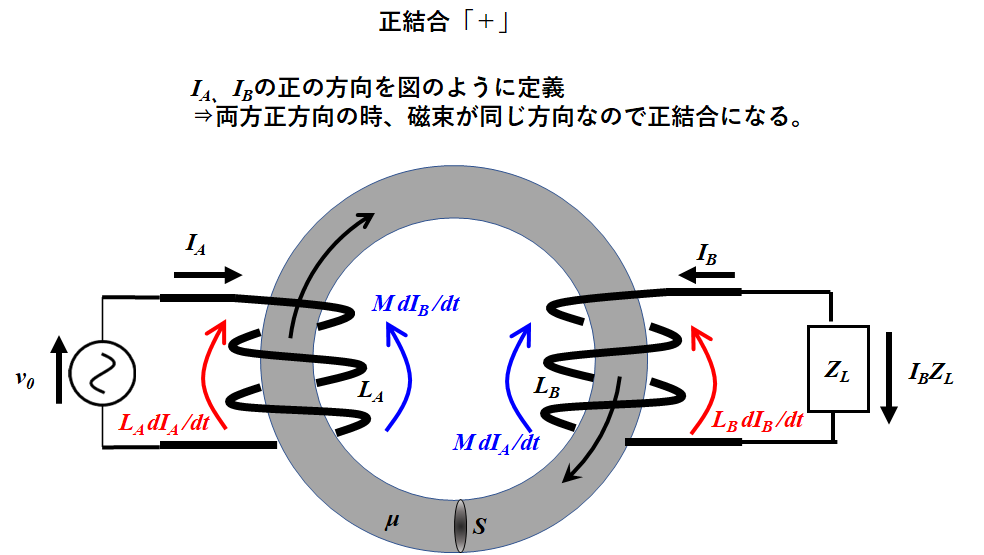
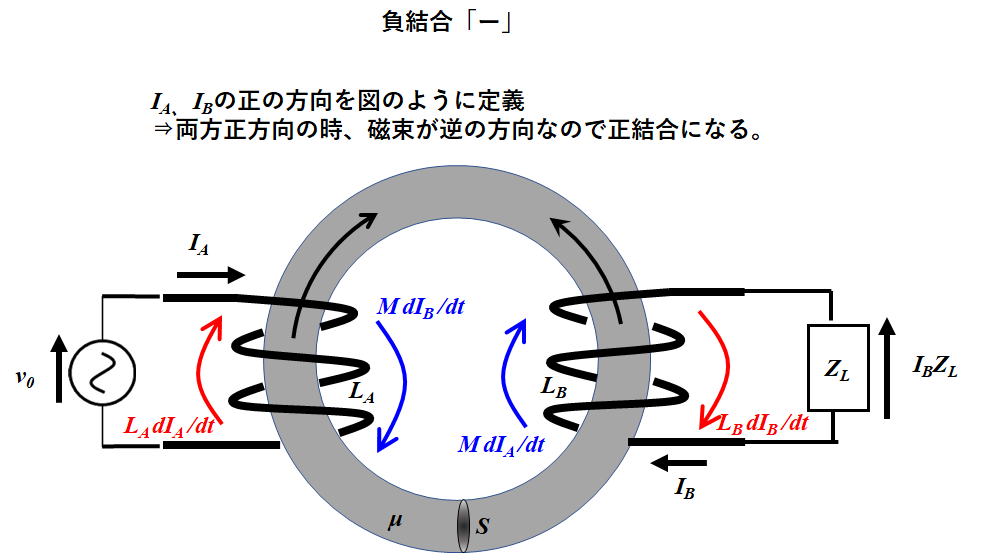
単一周波数ωに関する式で表したいので、\( {V}_{自己}=L \dfrac{dI}{dt}=jωL \) \( {V}_{相互}=M \dfrac{dI}{dt} =jωM\)とすると、キルヒホッフの式は、
\( {v}_{0}= jω{L}_{A}{I}_{A}±jω{M}{I}_{B} \)
\( 0 ={I}_{B}{Z}_{L}+ jω{L}_{B}{I}_{B}±jω{M}{I}_{A} \)
これらを解く。結合係数k=1の場合、\(M^2={L}_{A}{L}_{B}\)となることに注意すると、
\( {I}_{A}= \dfrac{(jω{L}_{B}+{Z}_{L}){v}_{0}}{ω^2(M^2-{L}_{A}{L}_{B})+jω{L}_{A}{Z}_{L}} \)
→ \( \dfrac{(jω{L}_{B}+{Z}_{L}){v}_{0}}{jω{L}_{A}{Z}_{L}} \)
\( {I}_{B}= \dfrac{∓jωM{v}_{0}}{ω^2(M^2-{L}_{A}{L}_{B})+jω{L}_{A}{Z}_{L}} \)
→ \( \dfrac{∓jωM{v}_{0}}{jω{L}_{A}{Z}_{L}} \)
トランスの電圧比・電流比・インピーダンス比・電力比
よく、ネット上でトランスの電圧比、電流比は巻き数比とどうたら、こうたら、と言われて図も与えられるが、1次側には電源があり、2次側には負荷があることを記載していない場合が多い。その場合、電圧比・電流比を導出することができない。なぜなら負荷をつなげてないと電流は流れないからである。仮にできたとしても誤魔化したような説明しかできないはずである。
以下では、上で用いた図から、電圧比・電流比、加えてインピーダンス比・電力比を求めていこうと思う。
上記の結果を用いれば、
電圧比
\( \dfrac{{V}_{B}}{{V}_{A}}=\dfrac{{I}_{B}{Z}_{L}}{{v}_{0}} =∓\dfrac{M}{{L}_{A}}= ∓\dfrac{{N}_{B}}{{N}_{A}} \)
電流比
\( \dfrac{{I}_{B}}{{I}_{A}}=\dfrac{∓jωM{v}_{0}}{(jω{L}_{B}+{Z}_{L}){v}_{0}}\)
→<\({Z}_{L}→0\)>→ \(\dfrac{∓jωM}{jω{L}_{B}} = ∓\dfrac{{N}_{A}}{{N}_{B}}\)
このように、電流比が巻き数の逆比になるには負荷\({Z}_{L}→0\)という極限下が必要だとわかる。
インピーダンス比
\( \dfrac{{R}_{B}}{{R}_{A}}=\dfrac{\dfrac{{I}_{B}{Z}_{L}}{{I}_{B}}}{\dfrac{{v}_{0}}{{I}_{A}}} =\dfrac{{Z}_{L}}{{v}_{0}} {I}_{A} = \dfrac{{Z}_{L}}{{v}_{0}} \dfrac{(jω{L}_{B}+{Z}_{L}){v}_{0}}{jω{L}_{A}{Z}_{L}}\)
→<\({Z}_{L}→0\)>→ \(\dfrac{jω{L}_{B}}{jω{L}_{A}}=\dfrac{{N}_{A}^2}{{N}_{B}^2} \)
このように、インピーダンス比が巻き数の2乗比になるには、負荷\({Z}_{L}→0\)という極限下が必要だとわかる。
ちなみにここは、\( \dfrac{{R}_{B}}{{R}_{A}}=\dfrac{\dfrac{{V}_{B}}{{I}_{B}}}{\dfrac{{V}_{A}}{{I}_{A}}}=\dfrac{{V}_{B}}{{V}_{A}}\dfrac{{I}_{A}}{{I}_{B}} \)の関係で証明してもよい。
電力比
\( \dfrac{{P}_{B}}{{P}_{A}} = \dfrac{{V}_{B}{I}_{B}}{{V}_{A}{I}_{A}} =(∓\dfrac{{N}_{B}}{{N}_{A}}) (∓\dfrac{{N}_{A}}{{N}_{B}}) =1 \)
この場合、電流比は負荷\({Z}_{L}→0\)という極限下のものを用いているので、こちらも負荷という存在と極限という条件が必要である。そもそも負荷がないと電力も発生しないので考えてみれば当たり前である。
まとめ
以上のように、トランスの公式とよく見かけるものは、負荷の存在などの暗黙の条件が必要となる。それが分かっていないと、ネット上に散見される導出が腑に落ちないだろう。ここで記した導出をぜひとも自分の手でやって理解を深めてほしい。
以上
