トランジスタ 電流増幅率α, β、遮断周波数、トランジション周波数、ICBO遮断電流
トランジスタの高周波特性
一アマ、一陸技、その他、技術系の世界では表題にあげたトランジスタの高周波特性の理解が求められる。
ただ、◎◎周波数や◎◎電流、遮断◎◎にはいろいろ名前があり、ややこしいので整理した。
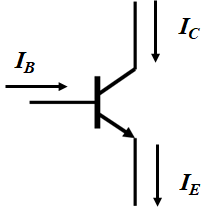
トランジスタの特性で重要なもの
一アマ、一陸技で理解しておいたほうがいいものを列挙した。
- 電流増幅率 \(α=\dfrac{d{i}_{c}}{d{i}_{e}}\)
- 電流増幅率 \(β=\dfrac{d{i}_{c}}{d{i}_{b}}\)
- 電流増幅率 α、βの関係 \( \dfrac{1}{α}=1+ \dfrac{1}{β}\)
- α遮断周波数 直流のときの増幅率に比べて3[dB](=真数でいうと\(1/\sqrt{2}\))ほど落ちる周波数
- β遮断周波数 直流のときの増幅率に比べて3[dB](=真数でいうと\(1/\sqrt{2}\))ほど落ちる周波数
- トランジション周波数
- コレクタ遮断電流 \({I}_{CBO}\)
以下で、それぞれの特性量を説明する。
電流増幅率 α
電流増幅率 \(α\) は、ベース接地回路において、入力電流の交流成分 \({i}_{e}\) の変化に対する出力電流 の交流成分\({i}_{c}\) の変化の割合である。
\(α=\dfrac{d{i}_{c}}{d{i}_{e}}\)
ベース接地限定での考え方であることに留意せよ。
以下で詳しく説明する。
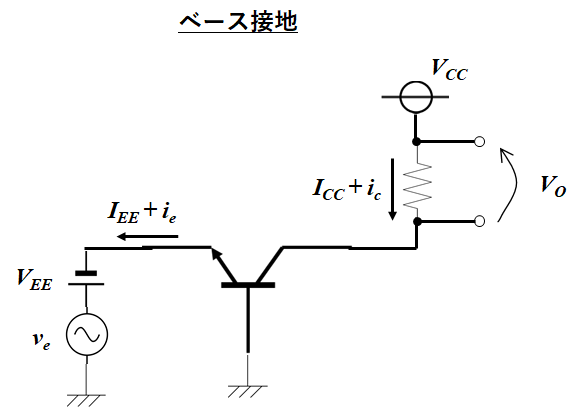
上記のベース接地回路において、入力はエミッタ電圧であり出力はコレクタ電圧である。
しかしトランジスタ自体は、電流増幅素子であるので本質的には電流の増幅率で議論を行う。
さらに、無線工学など高周波分野では、電気信号は交流の時間変化成分に乗せるため、電流の交流成分における増幅率で考えることが多いため、ここでも交流成分で議論する(直流成分の増幅率という考え方も存在する)。
トランジスタから見れば、
入力:エミッタ電流 \({I}_{E} = {I}_{EE}+{i}_{e}\) ただし\({I}_{EE}\)は直流成分、\({i}_{e}\)は交流成分とする。
出力:コレクタ電流 \({I}_{C} = {I}_{CC}+{i}_{c}\) ただし\({I}_{CC}\)は直流成分、\({i}_{c}\)は交流成分とする。
交流の信号の増幅回路においては、信号の時間変化幅がどれだけ増幅したかに興味があるので、電流増幅率αを以下のように考える。
\( α=\dfrac{\dfrac{d{I}_{C}}{dt}}{\dfrac{d{I}_{E}}{dt}} =\dfrac{\dfrac{d({I}_{CC}+{i}_{c})}{dt}}{\dfrac{d({I}_{EE}+{i}_{e})}{dt}} =\dfrac{\dfrac{d{i}_{c}}{dt}}{\dfrac{d{i}_{e}}{dt}}=\dfrac{d{i}_{c}}{d{i}_{e}} \)
このように、信号の直流成分の時間微分は0のため、結局交流成分の変化分の比で定義される。
電流増幅率 β
電流増幅率 \(β\) は、エミッタ接地回路において、入力電流の交流成分 \({i}_{b}\) の変化に対する出力電流 の交流成分\({i}_{c}\) の変化の割合である。
\(β=\dfrac{d{i}_{c}}{d{i}_{b}}\)
コレクタ接地限定での考え方であることに留意せよ。
以下で詳しく説明する。
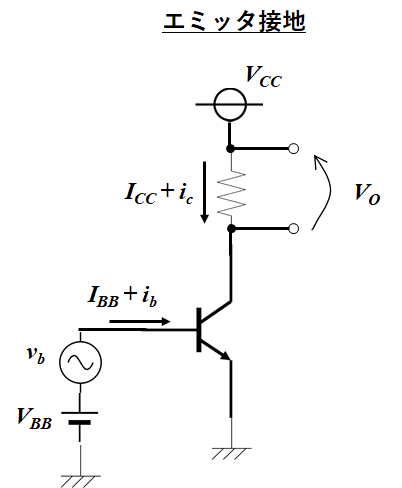
上記のコレクタ接地回路において、入力はベース電圧であり出力はコレクタ電圧である。
しかしトランジスタ自体は、電流増幅素子であるので本質的には電流の増幅率で議論を行う。
さらに、無線工学など高周波分野では、電気信号は交流の時間変化成分に乗せるため、電流の交流成分における増幅率で考えることが多いため、ここでも交流成分で議論する(直流成分の増幅率という考え方も存在する)。
トランジスタから見れば、
入力:ベース電流 \({I}_{B} = {I}_{BB}+{i}_{b}\) ただし\({I}_{BB}\)は直流成分、\({i}_{b}\)は交流成分とする。
出力:コレクタ電流 \({I}_{C} = {I}_{CC}+{i}_{c}\) ただし\({I}_{CC}\)は直流成分、\({i}_{c}\)は交流成分とする。
交流の信号の増幅回路においては、信号の時間変化幅がどれだけ増幅したかに興味があるので、電流増幅率αを以下のように考える。
\( β=\dfrac{\dfrac{d{I}_{C}}{dt}}{\dfrac{d{I}_{B}}{dt}} =\dfrac{\dfrac{d({I}_{CC}+{i}_{c})}{dt}}{\dfrac{d({I}_{BB}+{i}_{b})}{dt}} =\dfrac{\dfrac{d{i}_{c}}{dt}}{\dfrac{d{i}_{b}}{dt}}=\dfrac{d{i}_{c}}{d{i}_{b}} \)
このように、信号の直流成分の時間微分は0のため、結局交流成分の変化分の比で定義される。
電流増幅率 α、βの関係
上記より、
\(α=\dfrac{d{i}_{c}}{d{i}_{e}}\) …(1)
\(β=\dfrac{d{i}_{c}}{d{i}_{b}}\) …(2)
であり、トランジスタ電流(直流+交流)において、\( {I}_{E}={I}_{B}+{I}_{C} \)が成り立つ。
この式を両辺で時間微分すれば、
\( \dfrac{{I}_{E}}{dt}=\dfrac{{I}_{B}}{dt}+\dfrac{{I}_{C}}{dt} \)
直流成分の微分は0 ⇒ \( \dfrac{d{i}_{e}}{dt}=\dfrac{d{i}_{b}}{dt}+\dfrac{d{i}_{c}}{dt} \)
全微分形式で書き直す ⇒ \( d{i}_{e}=d{i}_{b}+d{i}_{c} \) …(3)
式(1) ~ (3)より以下のように変形できる。
\(α=\dfrac{d{i}_{c}}{d{i}_{e}} = \dfrac{d{i}_{c}}{d{i}_{b} + d{i}_{c}} = \dfrac{1}{\dfrac{d{i}_{b}}{d{i}_{c}} + 1}= \dfrac{1}{\dfrac{1}{β} + 1}\)
以上より、
\(α=\dfrac{1}{\dfrac{1}{β} + 1}\) ⇔ \( \dfrac{1}{α}=1+ \dfrac{1}{β}\)
α遮断周波数、β遮断周波数
上記で議論したように、α、βは
\(α=\dfrac{\dfrac{d{I}_{C}}{dt}}{\dfrac{d{I}_{E}}{dt}}=\dfrac{d{i}_{c}}{d{i}_{e}}\)
\(β=\dfrac{\dfrac{d{I}_{C}}{dt}}{\dfrac{d{I}_{B}}{dt}}=\dfrac{d{i}_{c}}{d{i}_{b}}\)
であるので、両方とも時間の関数である。すなわち\(α(t)\)、\(β(t)\)と書いたほうが正確である。
一方で高周波回路の分野では、回路の特性を周波数軸で見ることが多い。周波数\(ω\)の単一成分においでは、どうふるまうのか?周波数\(ω\)を変化させたら挙動はどう変わるのかが知りたいのだ。
よって、\(α(t)\)、\(β(t)\)をフーリエ変換して周波数\(ω\)の単一成分に直した、\(α(ω)\)、\(β(ω)\)を考えよう。今、増幅率を考えており、なおかつ\(α(ω)\)、\(β(ω)\)は複素数なのでこれらの振幅成分\(|α(ω)|\)、\(|β(ω)|\)を考える方が適切である。
\(|α(ω)|\)、\(|β(ω)|\)の周波数グラフを書くと一般には以下のようになる。
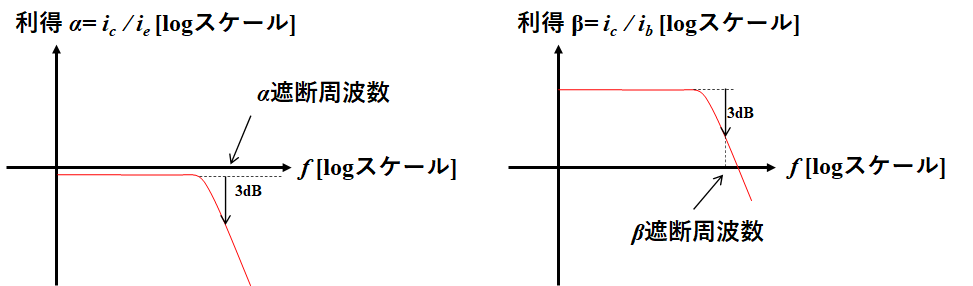
αはコレクタ電流とエミッタ電流の比であるから、直流ではほぼ1に近いかそれより小さい。なので対数グラフだと0[dB]か少しマイナスの部分からスタートである。
一方、βはコレクタ電流とベース電流の比であるから、直流では(\{h}_{FE}\)に近い。おおよそ100くらいなので対数グラフだと、40[dB]くらいからスタートである。
直流からスタートして、周波数が上がってもしばらくは増幅率は一定のままである。
しかし、ある地点から高周波になると増幅率は急激に落ち始めていく。
このとき、直流のときの増幅率に比べて3[dB](=真数でいうと\(1/\sqrt{2}\))ほど落ちる地点を遮断周波数といい、α、βの場合はα遮断周波数、β遮断周波数という。
遮断周波数は、それより高周波だとその増幅器が使えなくなるということを意味している。
トランジション周波数
トランジション周波数は、エミッタ接地の電流増幅率βに対してのみ定義される周波数であり、βが0[dB]になる周波数のことである。
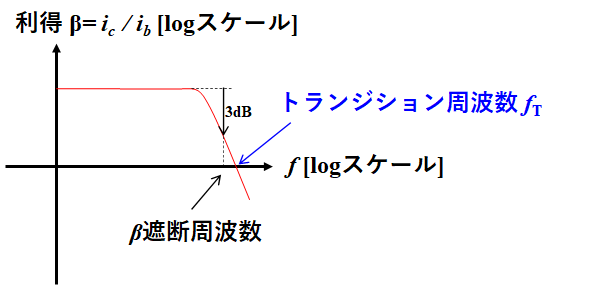
トランジション周波数は、平たく言えば増幅率が1、つまり入力電流と出力電流が同じ値になってしまう周波数のことである。これも同様、この周波数以上だと増幅器が機能しなくなることを意味する。
コレクタ遮断電流 \({I}_{CBO}\)
コレクタからベース方向への電流の漏れやすさの指標であり、定義はベースをショート、エミッタをオープンにして、コレクタ-ベース間に電圧をかけて測定された電流のことを言います。
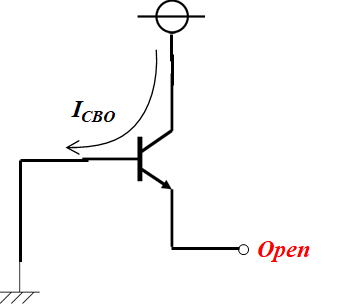
コレクタ遮断電流は、漏れ電流なので、小さいほうが特性の良いトランジスタと言えます。
ちなみに、\({I}_{CBO}\) のCBOの意味ですが、
C…コレクタ、B…ベース、E…エミッタとし、CBEの順番に並べる。今回はエミッタEがOpenなのでE⇒Oと書き換えて、CBOという表記ルールになっています。
以上
