【一陸技】工学A 令和5年1月期第1回 A-8 解説
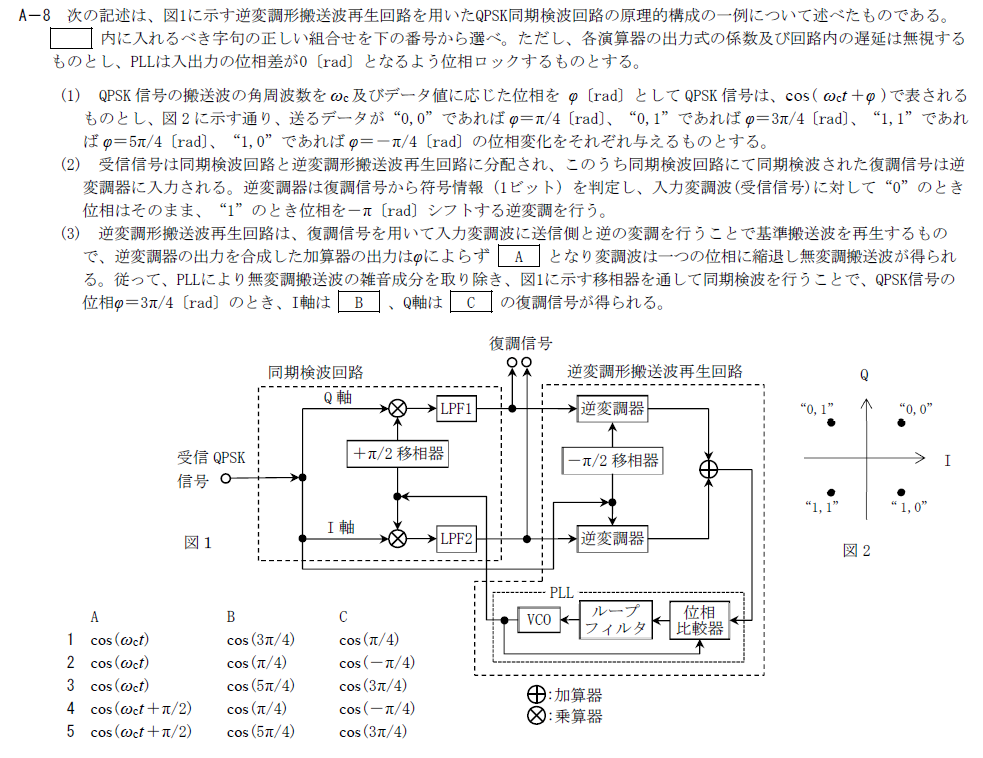
QPSK同期検波の問題である。同期検波とは受信波 A(t) cos(ωct + θ(t))から位相変化と振幅変化を取り除いた、綺麗なcos(ωct)を取り出して、それを局部発振器として用いる手法である。
令和に入ってからの一陸技では頻出問題なので、初見の人はぜひ理解したいところ。
しかしこいつも結構ややこしいし、数式無しの文章で原理を書かれてもよく分からないと思うので、問題文を読みながら丁寧に数式と図を使って原理を追っていくことにする。
(1)
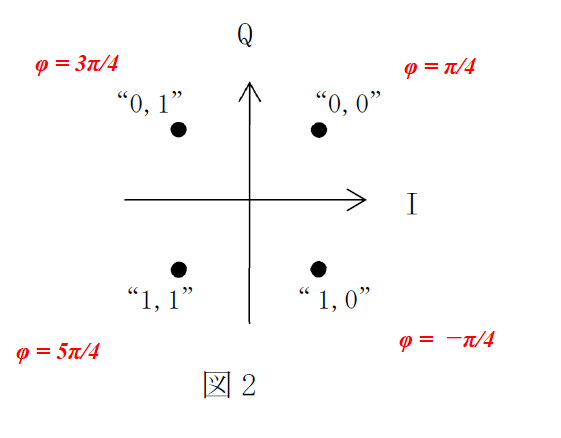
まずはこの問題におけるQPSK信号の定義から。図2にあるように、位相φの値と(I,Q)の値の対応が定義づけられている。実際、ここの対応付けはφに対して±2nπの不定性があるので問題や教科書によって定義が異なる。なので試験問題では毎回、位相と(I,Q)の対応付けの定義を確認することが必要だ。
図2より、変調された信号の時間波形は、以下のような数式になる。
Acos(ωct + φ) この振幅Aと位相φに情報(I,Q)が含まれている。
(2)
ここからは図を使って、入力された受信波Acos(ωct + φ)からどのように、信号が取り出されていくかを見ていく。
図中の①~⑨と信号式が変化していくのを以下で証明していく。
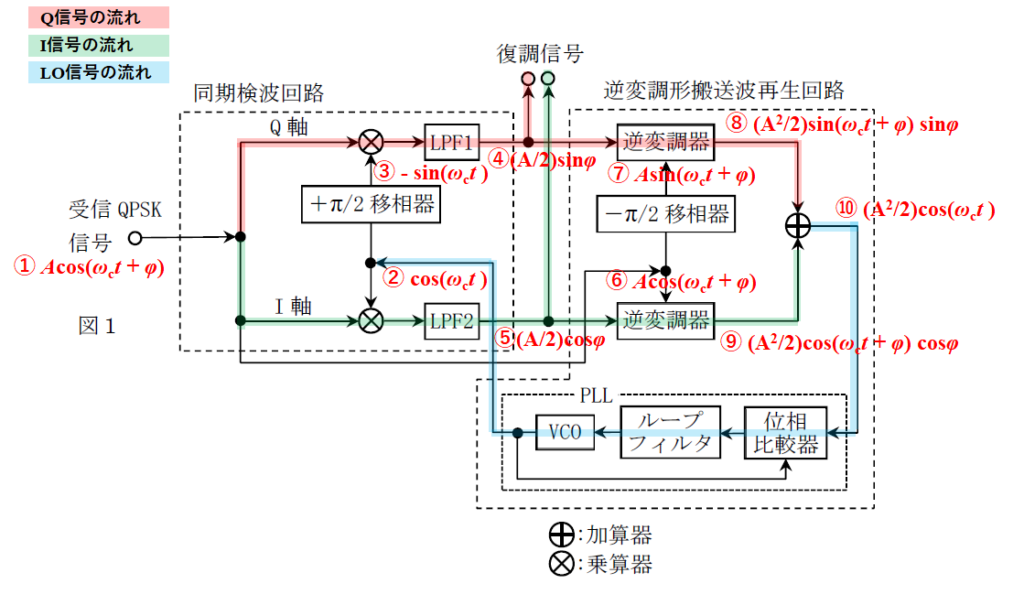
① 問題文中にあるように、QPSKの受信波を Acos(ωct + φ) と仮定する。
② 先回りすることになるが、LO信号は位相と振幅が取り除かれた cos(ωct) となる。
③ ②の信号は+π/2移相器を通るため、cos(ωct +π/2) = – sin(ωct)
④ Q軸信号はまず、③のLO信号と掛算され、LPFを通ってQ信号が取り出される
Acos(ωct + φ) × {- sin(ωct)}
= – Asin(ωct)cos(ωct + φ)
= – (A/2) * { sin(2ωct + φ) + sin(-φ) } ※積和の公式
→(LPFで2ωcをカット)→ (A/2)sinφ = Q
⑤ I 軸信号はまず、②のLO信号と掛算され、LPFを通って I 信号が取り出される
Acos(ωct + φ) × cos(ωct)
= Acos(ωct + φ)cos(ωct)
= (A/2) * { cos(2ωct + φ) + cos(φ) } ※積和の公式
→(LPFで2ωcをカット)→ (A/2)cosφ = I
⑥ 逆変調して搬送波を再生させるために、入力信号Acos(ωct + φ) をそのまま取ってくる。
⑦ 搬送波再生用の直交波を作るために、⑥を-π/2移相器通して、Acos(ωct + φ -π/2) = Asin(ωct + φ) を用意
⑧ 逆変調は単に④と⑦を掛算するだけ。(A2/2)sin(ωct + φ) sinφ
⑨ 逆変調は単に⑤と⑥を掛算するだけ。(A2/2)cos(ωct + φ) cosφ
⑩ ⑧と⑨を足す
(A2/2)cos(ωct + φ) cosφ + (A2/2)sin(ωct + φ) sinφ
= (A2/2)cos(ωct ) ※cosの加法定理でまとめる
さて、長くなったが問題を解いていく。この手の問題は落ち着いて処理を追っていくことが重要である。
[A]
逆変調出力の2つの和は⑩に書いたように(A2/2)cos(ωct )となるが、振幅は気にしなくてもOK。なのでcos(ωct )が答え。
[B]
φ = 3π/4 のとき、I軸の信号は⑤ I = (A/2)cosφ より cos(3π/4)
[C]
φ = 3π/4 のとき、I軸の信号は④ Q = (A/2)sinφ より sin(3π/4) = sin(π/2+π/4) = cos(π/4)
以上より、答えは1である。
