【一陸技】工学A 令和5年1月期第1回 A-5 解説

OFDM(職工周波数分割多重)の復調に関する問題である。この分野は離散フーリエ変換、単一矩形波のスペクトル、直行変調など、理解しておかねばならない基礎事項が山盛りで初心者には敷居が高い。一方で、近年ではOFDMは地デジ、Wifi, LTE, 5Gなどで使われており、マルチパス干渉に強い変調方式なので、一陸技でも令和になってから頻繁に出るようになった。
ただし、この問題は深いことを理解していなくても解ける。問題文をしっかり読めば単なる計算問題だということが分かるだろう。
それでは問題を解いていく。順番に問題文を読んでいきながら、数式を展開していく。
■(1) OFDMは多数のキャリア周波数を用いて伝送する。多数のキャリア周波数は、図で描かれているようにfs刻みでN個並べられている。
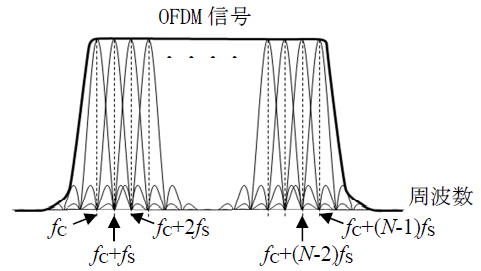
この 0番目 ~ (N-1)番目のうち、n番目のキャリア信号について数式化していく。n番目の搬送波周波数は(fc + nfs)。送信側ではこれに、2つのデータan, bn が直交変調で乗せられているので、送信波は以下のようになる。
an cos{ 2π(fc + nfs) t} – bn sin{ 2π(fc + nfs) t}
これを、n = 0 ~ N-1 まで足し合わせると、上の図全ての時間波形は次のようになる(問題文通り)。
S(t) = Σ[n=0 ~ N-1] [ an cos{ 2π(fc + nfs) t} – bn sin{ 2π(fc + nfs) t} ]
■(2) 上のS(t)を直交復調する場合は、搬送波周波数fcで直交復調せよ、と書かれてある。
従って、復調後のI信号、Q信号は以下のようになる(ここまでも問題文通り)
I信号 : S(t) × cos( 2πfc t) → 三角関数積和公式 → ローパスフィルタで低周波のみ取り出すと、、、
SBI(t) = Σ[n=0 ~ N-1] { an cos( 2π*n*fs t) – bn sin( 2π*n*fs t) }
Q信号 : S(t) × {- sin( 2πfc t)} → 三角関数積和公式 → ローパスフィルタで低周波のみ取り出すと、、、
SBQ(t) = Σ[n=0 ~ N-1] { an sin( 2π*n*fs t) + bn cos( 2π*n*fs t) }
■(3) 複素ベースバンドOFDM信号u(t)を計算する。問題文にもあるように、u(t) = SBI(t) + j SBQ(t) とあるので、上記のSBI(t) 、SBQ(t) を使って計算するだけである。従って、
u(t) = SBI(t) + j SBQ(t)
= Σ[n=0 ~ N-1] [ (an + jbn) {cos( 2π*n*fs t) + j sin( 2π*n*fs t) }]
・・・①
よって、[A]は (an + jbn) {cos( 2π*n*fs t) + j sin( 2π*n*fs t) }
さらに、オイラーの公式を用いて、exp(jθ)形式にする、dn = an + j bn を用いると、
u(t) = Σ[n=0 ~ N-1] dn exp( j 2π*n*fs t )
さらに、t = k/Nfs を代入して標本化すると、
u(k/Nfs) = Σ[n=0 ~ N-1] dn exp( j 2π*nk/N ) ・・・②
よって[B]の答えはj 2π*nk/N
※ここまでは問題文の通り計算するだけであるし、この時点で選択肢は1つに絞られる。
■(4) この本文を読む前に、フーリエ変換とフーリエ逆変換の違いを知っておかねばならない。
フーリエ変換:時間波形f(t)から周波数スペクトルF(ω)を求める。
F(ω) = (1/2π) ∫ dt f(t) exp(- jωt)
フーリエ逆変換:周波数スペクトルF(ω)から時間波形f(t)を求める。
f(t) = ∫ dω F(ω) exp(jωt)
これは、離散的にサンプリングした場合のフーリエ変換でも同じである。
今回、t = k/Nfs と離散化しているので、整数kは時間を意味する。ということは、整数nは周波数を意味することになり、式②は周波数スペクトルから時間波形を求めていることに相当する。よって、[C]は離散逆フーリエ変換。
②から複素振幅dnを取り出すには、離散フーリエ変換が必要。なぜなら整数nは周波数であり、複素振幅dnは周波数スペクトルのことだから。これは逆じゃない方のフーリエ変換である。よって、[D]は離散フーリエ変換。
フーリエ変換とフーリエ逆変換では、exp()の中身の符号が逆になる。よって、[E]は – j 2π*nk/N
以上より、答えは1である。
しっかり理解しようと思ったら結構難しいが、問題を解くだけなら問題文をしっかり読んで計算するだけ。しかも[A] ~ [E]のうち、2つか3つ分かれば答えが出る。
