【一陸技】工学A　令和5年1月期第1回　B-4 解説

2023-02-162023-12-09一陸技

振幅と位相が両方変調された波の復調過程に関する問題である。こちらの問題も、基本的には本文を読んでいきながら計算していくだけである。

(1)

元の搬送波をcos(ω_ct)としたとき、この搬送波の振幅をE₀(t)で振幅変調し、位相をφ₀(t)で位相変調すると、変調後の波は、E₀(t)cos{ω_ct + φ₀(t)}となる。受信機側ではこれを復調して情報E₀(t)、φ₀(t)を取り出す必要がある。

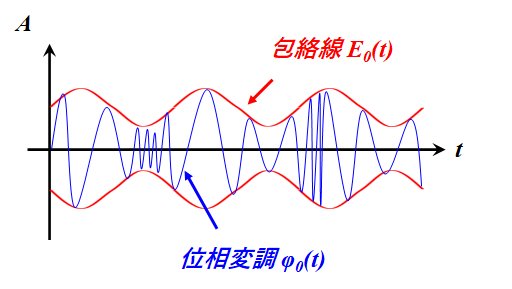
包絡線検波は、上の波形をLPFで平均化して周期の遅い包絡線成分E₀(t)だけを取り出す。従って、位相情報φ₀(t)は失われる([ア]=1)。

(2)

同期検波の場合は、上の波形に搬送波のきれいな波形を掛算してLPFを通すことで差周波数のみを取り出す方法である。

s₀(t)× s_s(t) = E₀(t)cos{ω_ct + φ₀(t)} × cos(ω_ct + θ_s)}

= (1/2) E₀(t) [ cos(θ_s – φ₀(t)) + cos{2ω_ct + φ₀(t) + θ_s }] ※積和の公式より　([イ]=7)

⇒（LPFで高周波成分除去([ウ]=5)）⇒　(1/2) E₀(t) cos(θ_s – φ₀(t)) 　　([エ]=8)

さらに、φ₀(t)=0のとき、出力は　(1/2) E₀(t) cos(θ_s) 　　([オ]=9)

θs = 0, π/2の2種類のLo信号で復調する方法がいわゆる直交復調であり、それを用いると、E₀(t)、φ₀(t)が同時に取得できる。

以上